course_model

Linear Regression

Linear Regression is our most important prediction tool. It uses multiple numerical independent variables to predict a single output/dependent variable. We generally use the OLS (ordinary least squares) algorithm.

Outcomes:

Links:

Good Resources:

Key concepts in regression

When to use Linear Regression:

Curve Fitting

Interpretation:

Weaknesses / Assumptions:

Step 1: Understand your data

Check field types and values

First we want to make sure that we understand our data. Begin by visually scanning the table. Then, use some functions to show what values are present in the data.

# Check field types and values
import pandas as pd
import numpy as np

# Sales table
df_raw = pd.DataFrame({
    'sales_id': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'sales_as_text': ['1,000', '2,000', '2,500', '10,000', '1,900', np.nan, '3,000', '4,000', '5,000', '6,000'],
    'profit': [0, 400, 1600, 6250, 240, np.nan, 900, 1600, 500, 600],
    'office_size': [16, 1, 2, 3, 1, 3, 2, 4, 5, 2],
    'closed': [True, False, True, False, False, False, True, True, False, True],
    'state': ['ca', 'ca', np.nan, 'NY', 'ca', np.nan, 'NY', 'NY', 'ca', 'ca'],
})

print("DataFrame dtypes:")
print(df_raw.dtypes)
df_raw.describe()

DataFrame dtypes:
sales_id           int64
sales_as_text     object
profit           float64
office_size        int64
closed              bool
state             object
dtype: object
sales_id profit office_size
count 10.00000 9.000000 10.000000
mean 5.50000 1343.333333 3.900000
std 3.02765 1922.862450 4.433459
min 1.00000 0.000000 1.000000
25% 3.25000 400.000000 2.000000
50% 5.50000 600.000000 2.500000
75% 7.75000 1600.000000 3.750000
max 10.00000 6250.000000 16.000000

Graph your data

You want to look for the distribution of values in each column, and the relationships between columns.

import matplotlib.pyplot as plt
import seaborn as sns

number_columns = df.select_dtypes(include=['number']).columns.tolist()
text_columns = df.select_dtypes(include=['object', 'category']).columns.tolist()

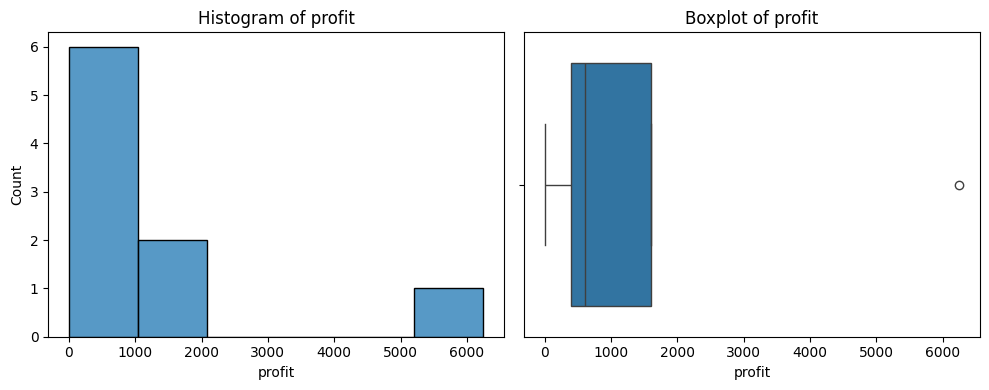
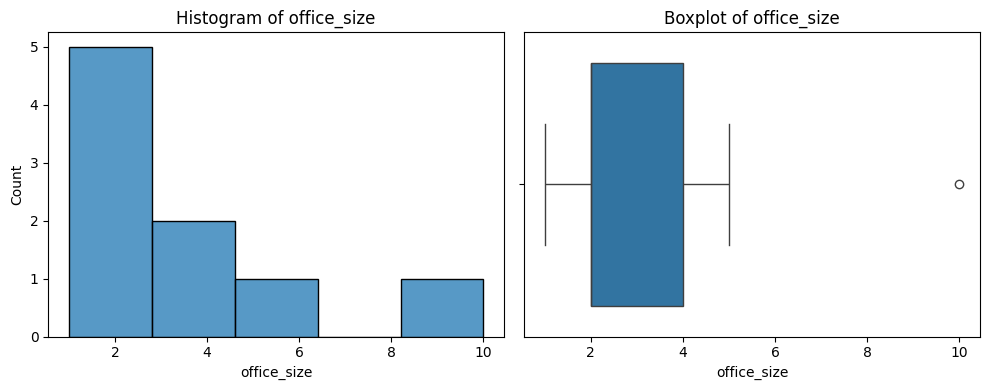
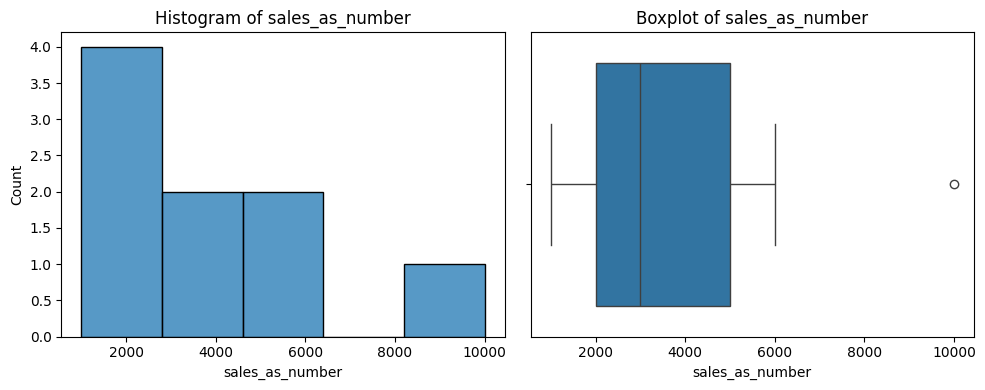
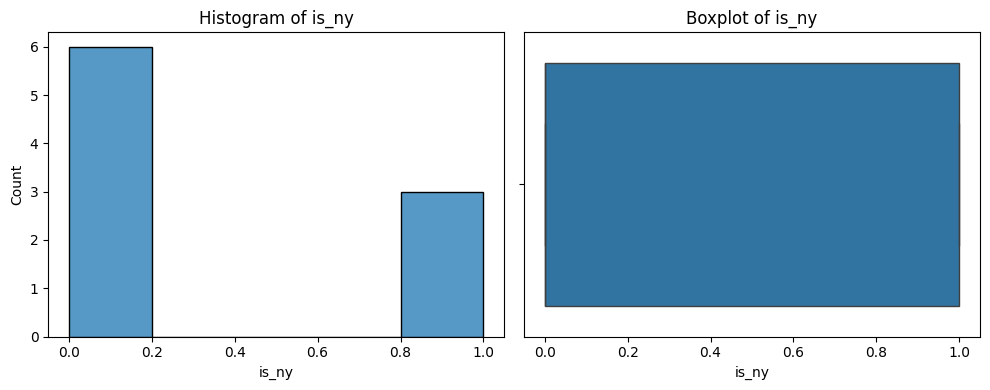
# Print a histogram and boxplot for each numeric column
for col in number_columns:
    plt.figure(figsize=(10, 4))
    plt.subplot(1, 2, 1)
    sns.histplot(df[col])
    plt.title(f'Histogram of {col}')
    
    plt.subplot(1, 2, 2)
    sns.boxplot(x=df[col].dropna())
    plt.title(f'Boxplot of {col}')
    
    plt.tight_layout()
    plt.show()

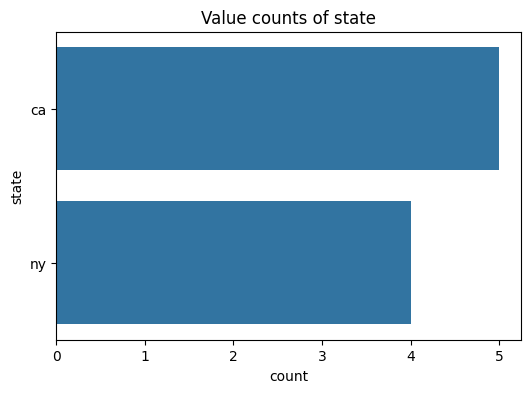
# Print a chart showing the distribution of values for each text column
for col in text_columns:
    plt.figure(figsize=(6, 4))
    sns.countplot(y=df[col], order=df[col].value_counts().index)
    plt.title(f'Value counts of {col}')
    plt.show()

png

png

png

png

png

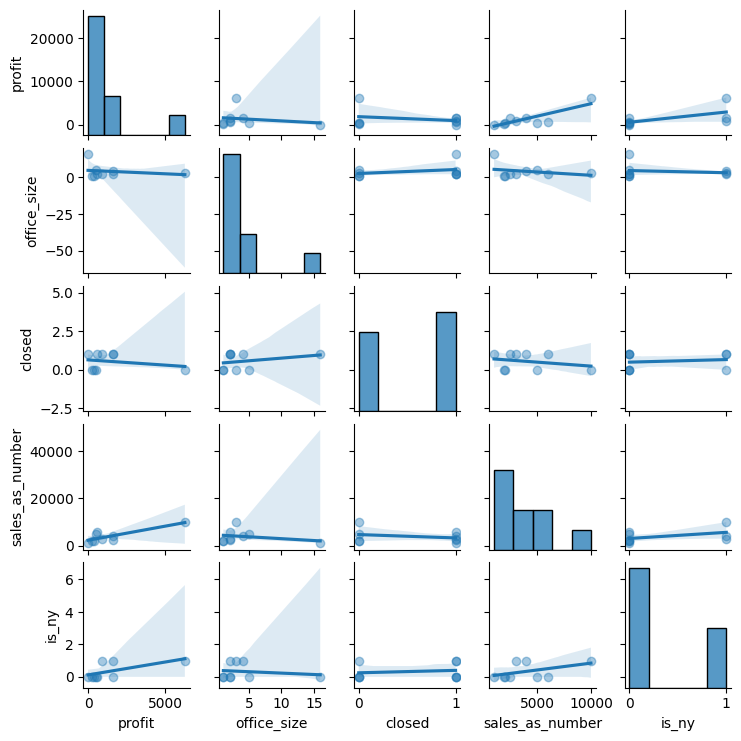
# Plot a pairs printout of each of the numeric variables
# Note that we use the alpha to set the visibility of the points to 0.01 to avoid overplotting. This also works well for large datasets.

sns.pairplot(df, kind='reg', height=1.5, plot_kws={'scatter_kws': {'alpha': 0.4}})
plt.show()

png

Step 2: Regression with Python

Key items:

import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf

X = df[['office_size', 'sales_as_number', 'is_ny']]
y = df['profit']

# Fit the model
X = sm.add_constant(X)  # Adds a constant term to the predictor
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
print(model.summary())



                            OLS Regression Results                            
==============================================================================
Dep. Variable:                 profit   R-squared:                       0.753
Model:                            OLS   Adj. R-squared:                  0.604
Method:                 Least Squares   F-statistic:                     5.071
Date:                Tue, 16 Dec 2025   Prob (F-statistic):             0.0562
Time:                        16:02:09   Log-Likelihood:                -74.009
No. Observations:                   9   AIC:                             156.0
Df Residuals:                       5   BIC:                             156.8
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
===================================================================================
                      coef    std err          t      P>|t|      [0.025      0.975]
-----------------------------------------------------------------------------------
const            -928.0026    949.517     -0.977      0.373   -3368.814    1512.809
office_size         2.5116    153.226      0.016      0.988    -391.367     396.391
sales_as_number     0.4813      0.176      2.734      0.041       0.029       0.934
is_ny            1109.9673    968.286      1.146      0.304   -1379.092    3599.027
==============================================================================
Omnibus:                        0.989   Durbin-Watson:                   0.450
Prob(Omnibus):                  0.610   Jarque-Bera (JB):                0.607
Skew:                           0.051   Prob(JB):                        0.738
Kurtosis:                       1.731   Cond. No.                     1.14e+04
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.14e+04. This might indicate that there are
strong multicollinearity or other numerical problems.

Step 3: Interpret results

Important parts of the summary output:

What explains each variable in our model?

RMSE

RMSE is the squared difference of each error. (https://www.statology.org/how-to-interpret-rmse/)[Link to a good reference]

Calculate the squared difference of each point, (10 - 10)^2 + (12 - 10)^2 + (8 - 10)^4 = 20

Divide by the number of observations, and take the square root. (20 / 3) ^ .5 = 2.58

Residuals

We may also want to see the difference between our prediction and actual values. (10 - 10), (12 - 10), (8 - 10) –> (0, 2, -2)

So, the RSME is the square root of the variance. This is the average distance between observed data values and predicted.

R-squared

The coefficient of determination tells us the proportion of variance in our dependent variable that can be explained by our independent variables.

It ranges from 0 to 1. Generally, the higher the number the better the prediction.

We will always use the adjusted R^2 when using multiple coeffients. This applies a small penalty for using additional columns.


# Calculate error metrics

# Find the residuals, which are the differences between the observed and predicted values
resid = model.resid

# The fitted values are the predicted values from the model
fitted = model.fittedvalues

# Calculate RMSE 
rmse_value = np.sqrt(np.mean(resid*resid))
print(f"RMSE: {rmse_value}")

# Calculate R²
r2_value = model.rsquared
print(f"R²: {r2_value}")

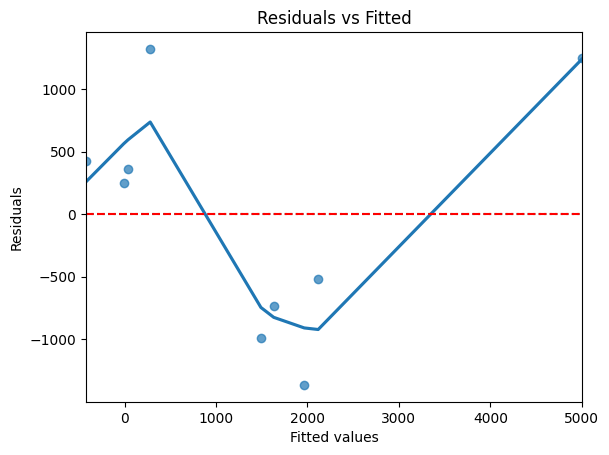
# Plot residuals
sns.residplot(x=fitted, y=resid, lowess=True, scatter_kws={'alpha': 0.7})
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted')
plt.axhline(0, color='red', linestyle='--')
plt.show()

RMSE: 901.6657510627008
R²: 0.7526298838455678

png